Граф — абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин. Например, за множество вершин можно взять множество аэропортов, обслуживаемых некоторой авиакомпанией, а за множество рёбер взять регулярные рейсы этой авиакомпании между городами.
Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах. Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа, в котором вершины — статьи, а дуги (ориентированные рёбра) — гиперссылки (тематическая карта).
Графы являются основным объектом изучения теории графов.
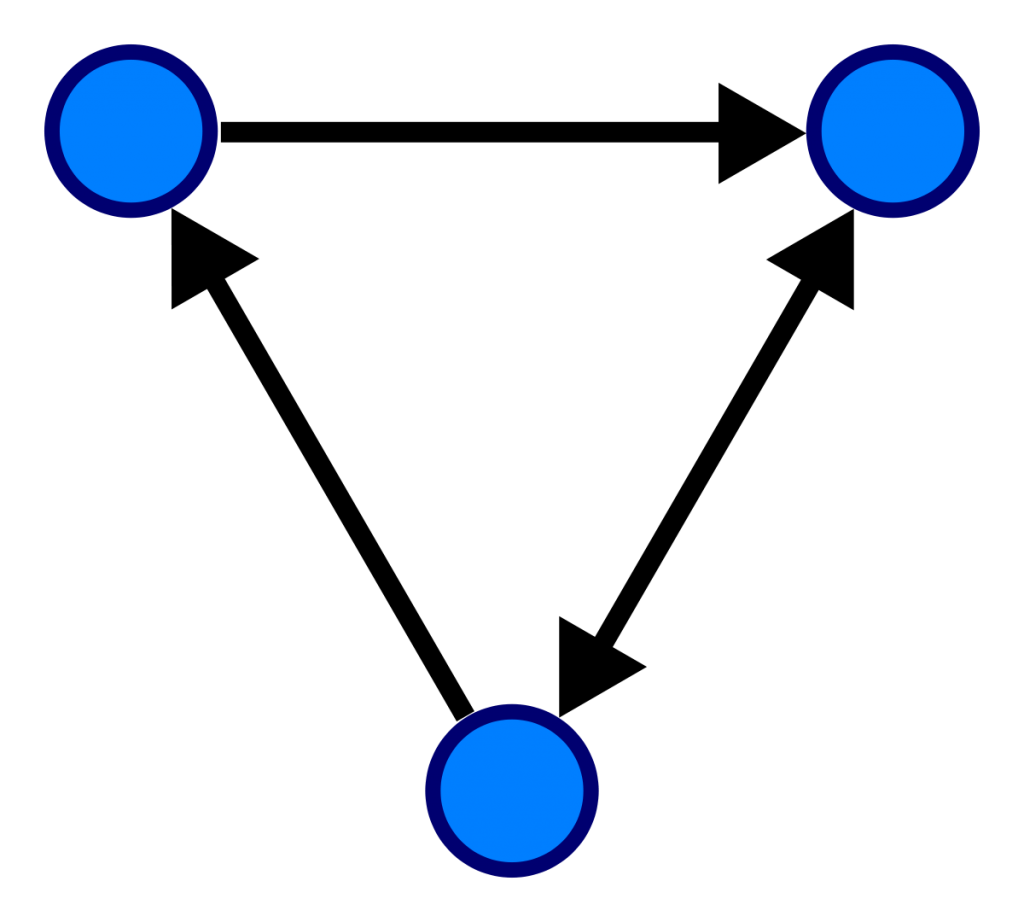
Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках и просто рёбрами. Граф, ни одному ребру которого не присвоено направление, называется неориентированным графом или неорграфом.
1. Создание ориентированного графа
Первое, что вам вероятно нужно изучить с точки зрения программирования с Boost graph, это использование списка смежности для создания соединений ребер графа. Вероятно, стоит привыкнуть к использованию typedef, учитывайте объявления Boost могут оказаться длинными.
Объявление списка смежности для ориентированного графа, пример:
typedef boost::adjacency_list<boost::vecS, boost::vecS, boost::directedS> DirectedGraph;
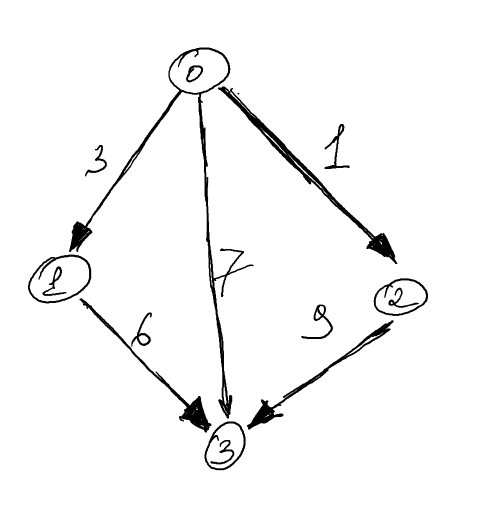
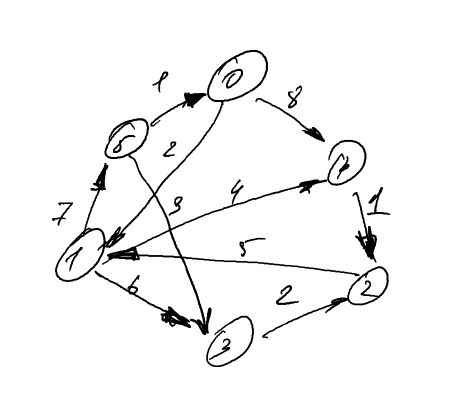
Предположим, мы хотим построить следующий взвешенный ориентированный граф:
Мы можем сделать это, делая повторные вызовы add_edge для создания графа. В следующем коде показано, как это можно сделать (не забудьте про -lboost_thread -lboost_system при сборке проекта) :
#include <boost/graph/adjacency_list.hpp>
#include <iostream>
typedef boost::property<boost::edge_weight_t, int> EdgeWeightProperty;
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS, boost::no_property, EdgeWeightProperty > DirectedGraph;
typedef boost::graph_traits<DirectedGraph>::edge_iterator edge_iterator;
int main()
{
DirectedGraph g;
boost::add_edge (0, 1, 3, g);
boost::add_edge (0, 2, 1, g);
boost::add_edge (0, 3, 7, g);
boost::add_edge (1, 3, 6, g);
boost::add_edge (2, 3, 9, g);
std::pair<edge_iterator, edge_iterator> ei = edges(g);
std::cout << "Количество ребер = " << num_edges(g) << "\n";
std::cout << "Список ребер:\n";
std::copy( ei.first, ei.second,
std::ostream_iterator<boost::adjacency_list<>::edge_descriptor>{
std::cout, "\n"});
std::cout << std::endl;
return 0;
}
Спискок смежности
template <class OutEdgeListS = vecS, // a Sequence or an AssociativeContainer
class VertexListS = vecS, // a Sequence or a RandomAccessContainer
class DirectedS = directedS,
class VertexProperty = no_property,
class EdgeProperty = no_property,
class GraphProperty = no_property,
class EdgeListS = listS>
class adjacency_list
: public detail::adj_list_gen<
adjacency_list<OutEdgeListS,VertexListS,DirectedS,
VertexProperty,EdgeProperty,GraphProperty,EdgeListS>,
VertexListS, OutEdgeListS, DirectedS,
VertexProperty, EdgeProperty,
GraphProperty, EdgeListS>::type,
// Support for named vertices
public graph::maybe_named_graph<
adjacency_list<OutEdgeListS,VertexListS,DirectedS,
VertexProperty,EdgeProperty,GraphProperty,EdgeListS>,
typename adjacency_list_traits<OutEdgeListS, VertexListS, DirectedS,
EdgeListS>::vertex_descriptor,
VertexProperty>
Получаем следующий результат:
Количество ребер = 5
Лист ребер:
(0,1)
(0,2)
(0,3)
(1,3)
(2,3)
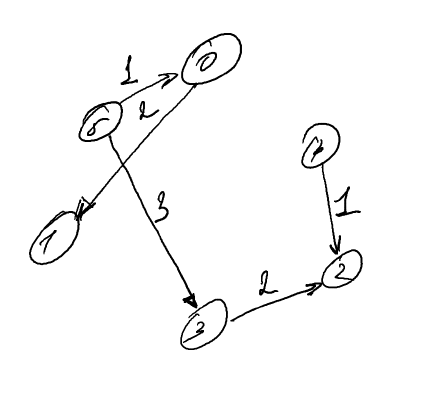
2. Создание неориентированного графа
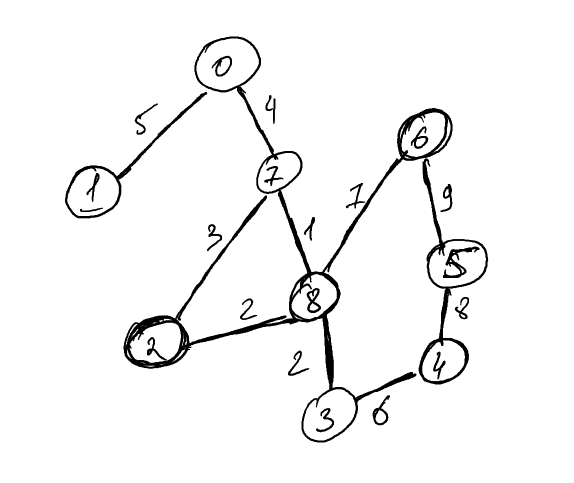
Пример неориентированного графа
Который мы строим аналогичным образом, но на этот раз предусматривая использование свойства boost:: undirectedS:
#include <boost/graph/adjacency_list.hpp>
#include <iostream>
typedef boost::property<boost::edge_weight_t, int> EdgeWeightProperty;
typedef boost::adjacency_list<boost::listS, boost::vecS,boost::undirectedS,boost::no_property,EdgeWeightProperty> UndirectedGraph;
typedef boost::graph_traits<UndirectedGraph>::edge_iterator edge_iterator;
int main()
{
UndirectedGraph g;
boost::add_edge (0, 1, 5, g);
boost::add_edge (0, 7, 4, g);
boost::add_edge (7, 2, 3, g);
boost::add_edge (7, 8, 1, g);
boost::add_edge (2, 8, 2, g);
boost::add_edge (8, 6, 7, g);
boost::add_edge (8, 3, 2, g);
boost::add_edge (6, 5, 9, g);
boost::add_edge (5, 4, 8, g);
boost::add_edge (3, 4, 6, g);
std::pair<edge_iterator, edge_iterator> ei = edges(g);
std::cout << "Количество ребер = " << num_edges(g) << "\n";
std::cout << "Список ребер:\n";
for (edge_iterator it = ei.first; it != ei.second; ++it )
{
std::cout << *it << std::endl;
}
std::cout << std::endl;
return 0;
}
Получаем следующий результат:
Количество ребер = 10
Список ребер:
(0,1)
(0,7)
(7,2)
(7,8)
(2,8)
(8,6)
(8,3)
(6,5)
(5,4)
(3,4)
3. Вывод веса ребер неориентированного графа
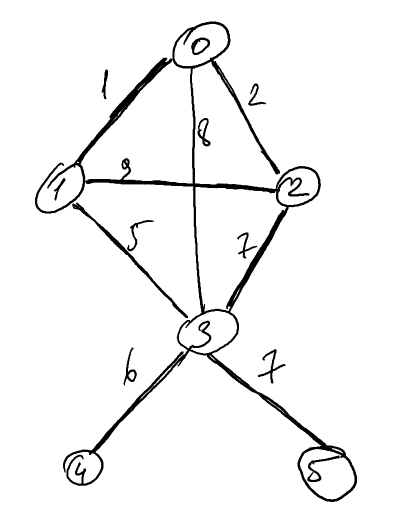
Рассмотрим следующее связующее дерево:
Получите отображение между ребрами и их соответствующими весами с помощью boost_property_map:
boost::property_map<UndirectedGraph, boost::edge_weight_t>::type EdgeWeightMap = get(boost::edge_weight_t(), g);
Полный код:
#include <boost/graph/adjacency_list.hpp>
#include <iostream>
typedef boost::property<boost::edge_weight_t, double> EdgeWeight;
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::undirectedS, boost::no_property, EdgeWeight> UndirectedGraph;
typedef boost::graph_traits<UndirectedGraph>::edge_iterator edge_iterator;
int main()
{
UndirectedGraph g;
boost::add_edge (0, 1, 1, g);
boost::add_edge (0, 2, 2, g);
boost::add_edge (1, 2, 9, g);
boost::add_edge (0, 3, 8, g);
boost::add_edge (1, 3, 5, g);
boost::add_edge (2, 3, 7, g);
boost::add_edge (3, 4, 6, g);
boost::add_edge (3, 5, 7, g);
boost::property_map<UndirectedGraph, boost::edge_weight_t>::type EdgeWeightMap = get(boost::edge_weight_t(), g);
std::pair<edge_iterator, edge_iterator> edgePair;
for (edgePair = edges(g); edgePair.first != edgePair.second; ++edgePair.first)
{
std::cout << *edgePair.first << " " << EdgeWeightMap[*edgePair.first] << std::endl;
}
return 0;
}
(0,1) 1
(0,2) 2
(1,2) 9
(0,3) 8
(1,3) 5
(2,3) 7
(3,4) 6
(3,5) 7
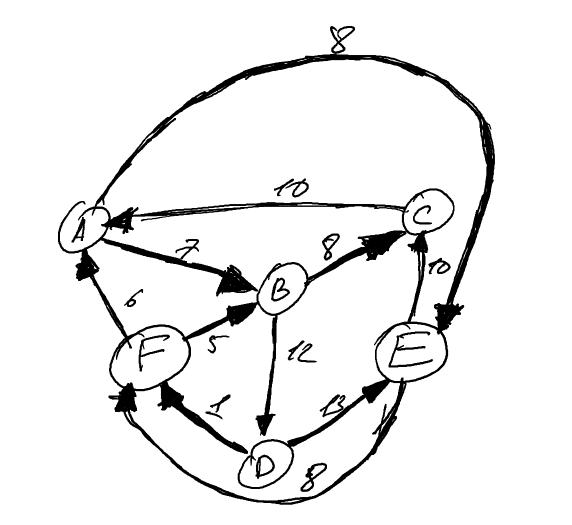
4. Нахождение минимального пути, алгоритм Дейкстры
Алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его используют протоколы маршрутизации OSPF и IS-IS.
В этой демонстрации мы используем метод dijkstra_shortest_paths для получения не только дерева кратчайших путей, но и вывода пути между выбранной парой источник-приемник.
#include <boost/config.hpp>
#include <iostream>
#include <fstream>
#include <boost/graph/graph_traits.hpp>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <boost/property_map/property_map.hpp>
int main(int, char *[])
{
typedef boost::adjacency_list <boost::listS, boost::vecS, boost::directedS, boost::no_property,
boost::property<boost::edge_weight_t, int> > graph_t;
typedef boost::graph_traits<graph_t>::vertex_descriptor vertex_descriptor;
typedef std::pair<int, int> Edge;
const int num_nodes = 6;
enum nodes { A, B, C, D, E, F };
char name[] = "ABCDEF";
Edge edge_array[] = {
Edge(C, A),
Edge(A, B),
Edge(A, E),
Edge(F, A),
Edge(B, C),
Edge(B, D),
Edge(E, C),
Edge(E, F),
Edge(D, F),
Edge(D, E),
Edge(F, B)
};
int weights[] = { 10, 7, 8, 6, 8, 12, 10, 8, 1, 13, 5 };
int num_arcs = sizeof(edge_array) / sizeof(Edge);
// Graph created from the list of edges
graph_t g(edge_array, edge_array + num_arcs, weights, num_nodes);
// Create property_map from edges to weights
boost::property_map<graph_t, boost::edge_weight_t>::type weightmap = get(boost::edge_weight, g);
// Create vectors to store the predecessors (p) and the distances from the root (d)
std::vector<vertex_descriptor> p(num_vertices(g));
std::vector<int> d(num_vertices(g));
// Create descriptor for the source node
vertex_descriptor s = vertex(A, g);
vertex_descriptor goal = vertex(F, g);
// Evaluate Dijkstra on graph g with source s, predecessor_map p and distance_map d
boost::dijkstra_shortest_paths(g, s,
boost::predecessor_map(&p[0]).distance_map(&d[0]));
//p[] is the predecessor map obtained through dijkstra
//name[] is a vector with the names of the vertices
//s and goal are vertex descriptors
std::vector<boost::graph_traits<graph_t>::vertex_descriptor > path;
boost::graph_traits<graph_t>::vertex_descriptor current = goal;
while(current!=s)
{
path.push_back(current);
current = p[current];
}
path.push_back(s);
// Prints the path obtained in reverse
std::cout << "Path from " << name[s] << " to " << name[goal] << std::endl;
std::vector<boost::graph_traits<graph_t>::vertex_descriptor >::reverse_iterator it;
for (it = path.rbegin(); it != path.rend(); ++it) {
std::cout << name[*it] << " ";
}
std::cout << std::endl;
return EXIT_SUCCESS;
}
Находим короткий путь между узлами A и F.
Путь A -> F
A E F
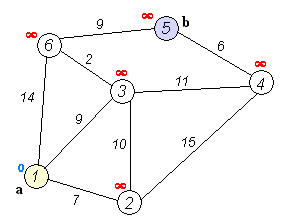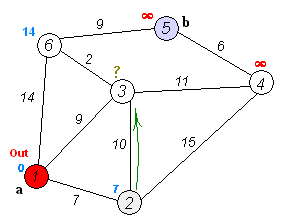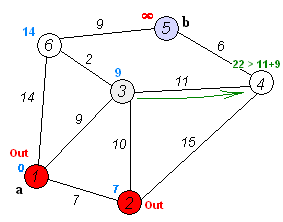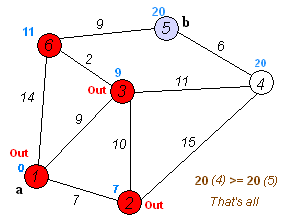
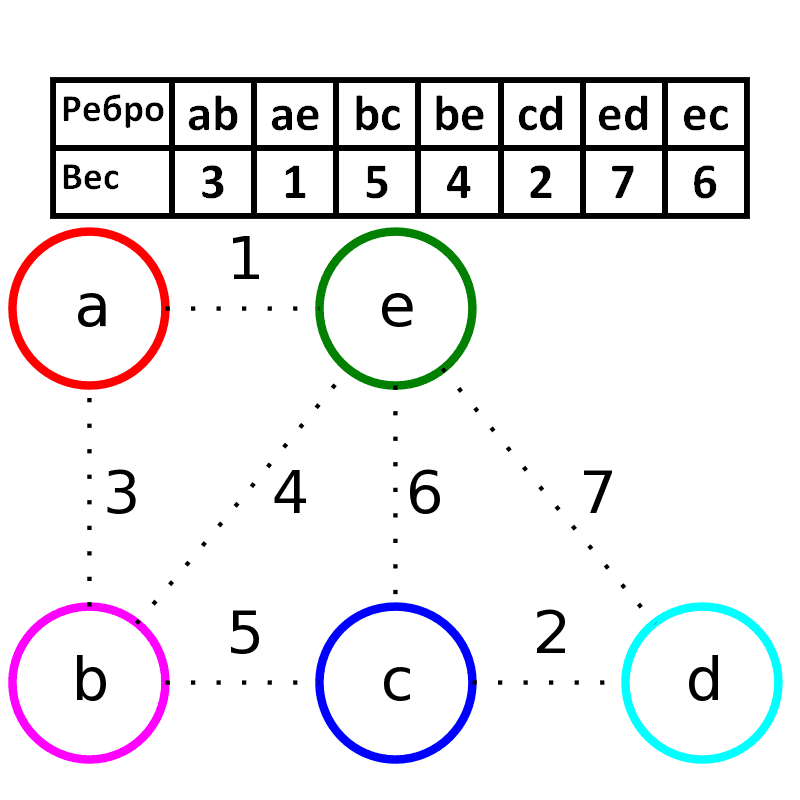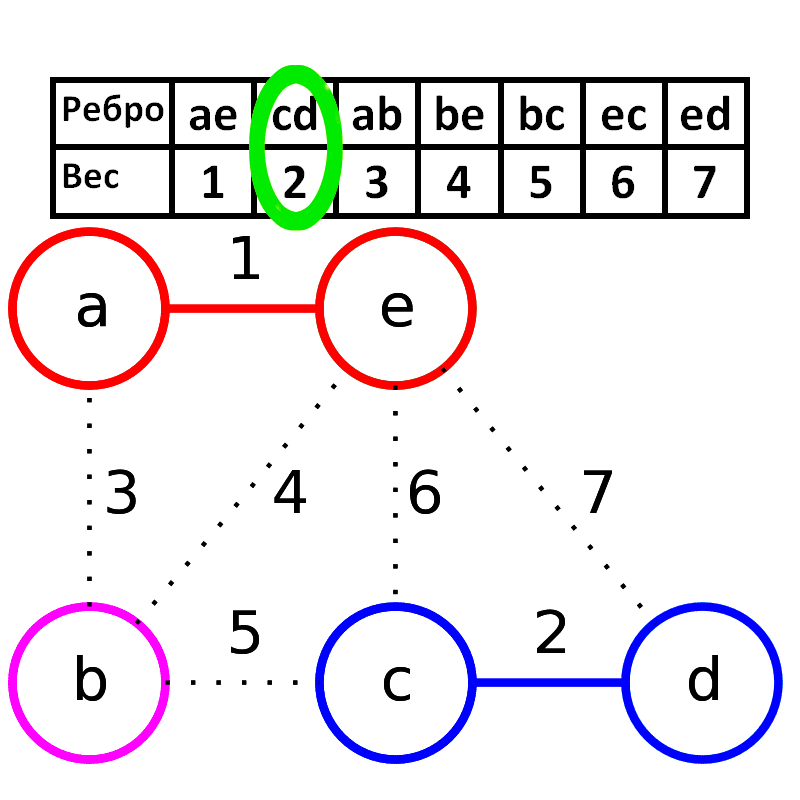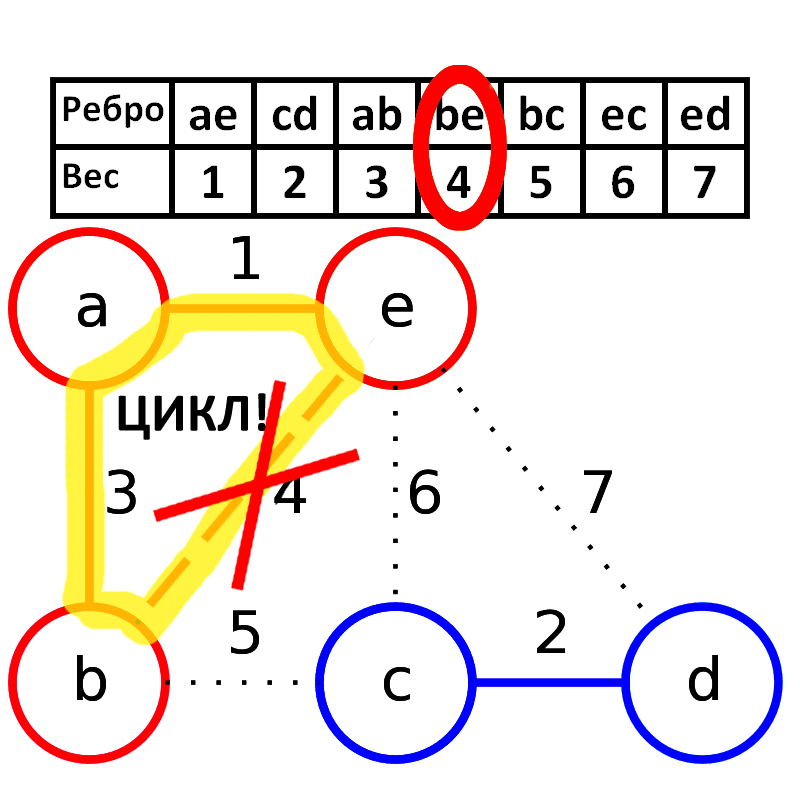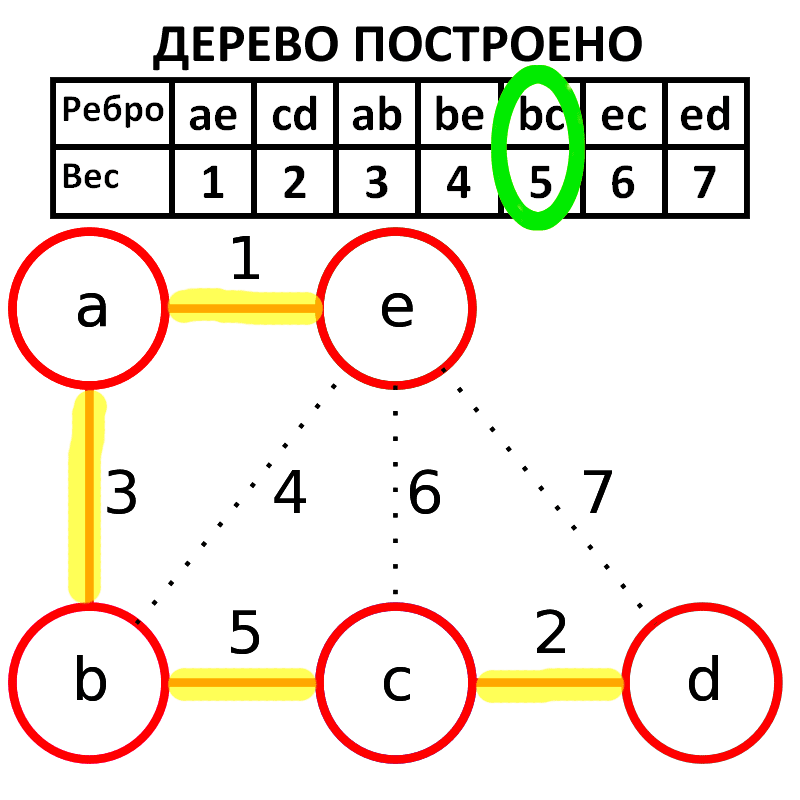
5. Поиск минимальных остовных деревьев с использованием алгоритма Крускала
Алгоритм Краскала — эффективный алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Также алгоритм используется для нахождения некоторых приближений для задачи Штейнера.
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/kruskal_min_spanning_tree.hpp>
#include <iostream>
#include <fstream>
int main()
{
typedef boost::adjacency_list< boost::vecS, boost::vecS, boost::undirectedS,
boost::no_property, boost::property<boost::edge_weight_t, int> > Graph;
typedef boost::graph_traits <Graph>::edge_descriptor Edge;
typedef boost::graph_traits <Graph>::vertex_descriptor Vertex;
typedef std::pair<int, int> P;
const int num_nodes = 6;
P edge_array[] = {
P(0, 4),
P(4, 2),
P(2, 1),
P(1, 5),
P(5, 0),
P(5, 3),
P(3, 2),
P(1, 3),
P(4, 1),
P(0, 1)
};
int weights[] = { 8, 1, 5, 7, 1, 3, 2, 6, 4, 2 };
std::size_t num_edges = sizeof(edge_array) / sizeof(P);
Graph g(edge_array, edge_array + num_edges, weights, num_nodes);
boost::property_map<Graph, boost::edge_weight_t >::type weight = get(boost::edge_weight, g);
std::vector < Edge > spanning_tree;
boost::kruskal_minimum_spanning_tree(g, std::back_inserter(spanning_tree));
std::cout << "Print the edges in the MST:" << std::endl;
for (std::vector < Edge >::iterator ei = spanning_tree.begin();
ei != spanning_tree.end(); ++ei)
{
std::cout << source(*ei, g)
<< " <--> "
<< target(*ei, g)
<< " with weight of "
<< weight[*ei]
<< std::endl;
}
return 0;
}
Минимальное остовное дерево:
4 < –> 2 вес 1
5 < –> 0 вес 1
3 < –> 2 вес 2
0 < –> 1 вес 2
5 < –> 3 вес 3
6. Проблема максимального потока DIMACS
DIMACS (Center for Discrete Mathematics and Theoretical Computer Science) – центр дискретной математики и теоретической информатики.
В теории оптимизации и теории графов, задача о максимальном потоке заключается в нахождении такого потока по транспортной сети, что сумма потоков из истока, или, что то же самое, сумма потоков в сток максимальна.
Задача о максимальном потоке является частным случаем более трудных задач, как например задача о циркуляции.
Пример задачи о максимальном потоке.
dimacs.txt
c This is a simple example file to demonstrate the DIMACS c input file format for maximum flow problems. The solution c vector is [5,10,5,0,5,5,10,5] with cost at 15. c Problem line (nodes, links) p max 6 8 c source n 1 s c sink n 6 t c Arc descriptor lines (from, to, capacity) a 1 2 5 a 1 3 15 a 2 4 5 a 2 5 5 a 3 4 5 a 3 5 5 a 4 6 15 a 5 6 5 c c End of file
Строки, начинающиеся с “c”, являются строками комментариев. Строка задачи начинается с буквы “p” и представляет обозначение задачи (max, min и т. д.), количество ребер (8) и количество вершин (6). Строки, начинающиеся с “n”, являются дескрипторами узла-идентификатора – узел ID и является ли узел источником (“s”) или приемником (“t”). Наконец, строки “a” являются дескрипторами, дающими взаимосвязи узлов и их весового значения. В следующем графическом представлении примера задачи сетевого потока показаны не только сетевые соединения и веса, но и потоки на каналах:
#include <boost/config.hpp>
#include <iostream>
#include <fstream>
#include <string>
#include <boost/graph/edmonds_karp_max_flow.hpp>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/read_dimacs.hpp>
#include <boost/graph/graph_utility.hpp>
int main()
{
typedef boost::adjacency_list_traits<boost::vecS, boost::vecS, boost::directedS > Traits;
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS,
boost::property<boost::vertex_name_t, std::string >,
boost::property<boost::edge_capacity_t, long,
boost::property<boost::edge_residual_capacity_t, long,
boost::property<boost::edge_reverse_t, Traits::edge_descriptor>>>> Graph;
Graph g;
boost::property_map<Graph, boost::edge_capacity_t>::type
capacity = get(boost::edge_capacity, g);
boost::property_map<Graph, boost::edge_reverse_t>::type rev = get(boost::edge_reverse, g);
boost::property_map<Graph, boost::edge_residual_capacity_t>::type
residual_capacity = get(boost::edge_residual_capacity, g);
Traits::vertex_descriptor s, t;
// Use a DIMACS network flow file as stdin:
std::ifstream is ("dimacs.txt", std::ios::in);
read_dimacs_max_flow(g, capacity, rev, s, t, is);
#if defined(BOOST_MSVC) && BOOST_MSVC <= 1300
std::vector<default_color_type> color(num_vertices(g));
std::vector<Traits::edge_descriptor> pred(num_vertices(g));
long flow = edmunds_karp_max_flow
(g, s, t, capacity, residual_capacity, rev, &color[0], &pred[0]);
#else
long flow = edmonds_karp_max_flow(g, s, t);
#endif
std::cout << "c The total flow:" << std::endl;
std::cout << "s " << flow << std::endl << std::endl;
std::cout << "c flow values:" << std::endl;
boost::graph_traits<Graph>::vertex_iterator u_iter, u_end;
boost::graph_traits<Graph>::out_edge_iterator ei, e_end;
for (boost::tie(u_iter, u_end) = vertices(g); u_iter != u_end; ++u_iter)
for (boost::tie(ei, e_end) = out_edges(*u_iter, g); ei != e_end; ++ei)
if (capacity[*ei] > 0)
std::cout << "f " << *u_iter << " " << target(*ei, g) << " "
<< (capacity[*ei] - residual_capacity[*ei])
<< std::endl;
return EXIT_SUCCESS;
}
c Общий поток:
s 15
c значения потока:
f 0 1 5
f 0 2 10
f 1 3 5
f 1 4 0
f 2 3 5
f 2 4 5
f 3 5 10
f 4 5 5
Как и предполагалось, вектор решения выходных переменных составляет [5, 10, 5, 0, 5, 5, 10, 5].